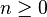数学之家

标题: 什么叫“广义伯努力不等式”呢 [打印本页]

---

作者: kuing    时间: 2009-8-20 21:49
标题: 什么叫“广义伯努力不等式”呢
话说早前在某地看到某人在证明某不等式时提到这个东东，想问一下这个东东是怎么样的，一般地描术下？

---

作者: 高斯门徒    时间: 2009-8-26 10:11


伯努利不等式是说：对任意整数，和任意实数，
； 如果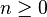是偶数，则不等式对任意实数x成立。
可以看到在n = 0,1，或x = 0时等号成立，而对任意正整数和任意实数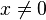，，有严格不等式：

证明和推广
伯努利不等式可以用数学归纳法证明：当n = 0,1，不等式明显成立。假设不等式对正整数n，实数时成立，那么
。 下面是推广到实数幂的：如果x > − 1，那么：
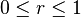若或，有； 若，有。 这不等式可以用比较来证明：
当r = 0,1时，等式显然成立。
在上定义f(x) = (1 + x)r − (1 + rx)，其中， 对x微分得f'(x) = r(1 + x)r − 1 − r， 则f'(x) = 0当且仅当x = 0。分情况讨论：

• 0 < r < 1，则对x > 0，f'(x) < 0；对 − 1 < x < 0，f'(x) > 0。因此f(x)在x = 0时取最大值0，故得。
• r < 0或r > 1，则对x > 0，f'(x) > 0；对 − 1 < x < 0，f'(x) < 0。因此f(x)在x = 0时取最小值0，故得。

在这两种情况，等号成立当且仅当x = 0。

  

---

作者: kuing    时间: 2009-8-26 11:48
楼上说的这个我知道啊，是常识了。

不过注意我要问的是，“广义”。。。

---

作者: EMP震荡波    时间: 2009-8-26 13:50
“广义”就是把正整数n换成实数r

---

作者: kuing    时间: 2009-8-27 10:33
4# EMP震荡波

不是

其实一般说的伯努力不等式的指数就是实数

而且那里用的能看得出是另一种形式

---

作者: monkey121    时间: 2009-8-30 00:26
虽然可能同样不是你要的那种，但好歹找了资料，放在这里给大家看看吧：

伯努利不等式

基本概念
　　数学中的伯努利不等式是说：对任意整数，和任意实数，
　　；如果是偶数，则不等式对任意实数x成立。
　　可以看到在n = 0,1，或x = 0时等号成立，而对任意正整数和任意实数，，有严格不等式：
　　。伯努利不等式经常用作证明其他不等式的关键步骤。

证明
　　设x＞-1,且x≠0,n是不小于2的整数,则(1+x)^n≥1+nx.
　　证明:
　　用数学归纳法:
　　当n=1,上个式子成立,
　　设对n-1,有:
　　(1+x)^(n-1)>=1+(n-1)x成立,
　　则
　　(1+x)^n
　　=(1+x)^(n-1)(1+x)
　　>=[1+(n-1)x](1+x)
　　=1+(n-1)x+x+(n-1)x^2
　　>=1+nx
　　就是对一切的自然数,当
　　x>=-1,有
　　(1+x)^n>=1+nx
　　下面把伯努利不等式推广到实数幂形式：
　　若r ≤0或r ≥ 1，有(1+x)^r ≥ 1 + rx
　　若0 ≤ r ≤ 1，有(1+x)^r ≤ 1 + rx
　　这个不等式可以直接通过微分进行证明，方法如下：
　　如果r=0，1，则结论是显然的
　　如果r≠0，1，作辅助函数f(x)=(1+x)^r-(1+rx), 那么f'(x)=r*(1+x)^(r-1)-r, 则f'(x)=0 <==> x=0;
　　下面分情况讨论：
　　1. 0 < r < 1，则对于x > 0，f'(x) < 0；对于 − 1 < x < 0，f'(x) > 0。因此f(x)在x = 0处取最大值0，故得(1+x)^r ≤ 1+rx。
　　2. r < 0或r > 1，则对于x > 0，f'(x) > 0；对于 − 1 < x < 0，f'(x) < 0。因此f(x)在x = 0处取最小值0，故得(1+x)^r ≥ 1+rx
　　证毕

---

作者: 石崇的BOSS    时间: 2009-8-30 20:48
圣手，我算是服了你了，还某地某人证明某不等式……

---

作者: 里亦维奇    时间: 2009-8-30 21:12
证明广义伯努利不等式：

---

作者: kuing    时间: 2009-8-30 22:23

圣手，我算是服了你了，还某地某人证明某不等式……
石崇的BOSS 发表于 2009-8-30 20:48

---

作者: PaulErdos    时间: 2010-5-9 22:30

证明广义伯努利不等式：
**** 本内容被作者隐藏 ****
里亦维奇 发表于 2009-8-30 21:12

在狭义的Bernoulli's inequality里面的n∈R，但为什么在证明广义的时候n∈n了呢？

---

作者: 左眼的风景    时间: 2010-10-5 22:34
1# kuing   应该是对于任意a[sub]I[/sub]，≥－1，（1+a[sub]1[/sub]）（1+a[sub]2[/sub]）...(1+a[sub]n[/sub])≥1+a[sub]1[/sub]+a[sub]2[/sub]...+a[sub]n[/sub]

---

作者: 左眼的风景    时间: 2010-10-5 22:35
7# 石崇的BOSS 怎么证明？

---

作者: 石崇的BOSS    时间: 2010-10-5 22:41
12# 左眼的风景
8楼已经证明……

---

欢迎光临 数学之家 (http://www.2math.cn/)

Powered by Discuz! X3.1